Afstand houden – oplossing 3
D.J. Bolt
12-02-22
Een lezer bood ons een geniale oplossing aan voor het probleem hoe je zes patiënten in de dokterswachtkamer van 2 bij 2 meter zou moeten plaatsen. Dachten wij horizontaal als mensen met de voeten op de grond, hij kwam met een driedimensionale oplossing: de eerste drie gewoon om maximale afstand van elkaar op de grond en de volgen drie op hoge stoelen. Prachtig!
Maar de vraag die bleef prangen was wel, hoe hoog moeten dan die zetels minimaal zijn om te waarborgen dat ook zij die zo in hoogheid zijn gezeten minstens anderhalve meter afstand van elkaar bewaren. Het zoeken naar antwoord op die vraag bleef ons bezig houden.
En eureka!, we denken het te hebben gevonden. We willen het graag uitleggen voor hen die van rekenen houden en andere nieuwsgierigen.
Minimale hoogte stoeltjes h1 en h3
In figuur 1 geven we de situatie weer in de wachtkamer. Jantje, Pietje en Klaasje, die in vorige oplossingen al eerder tegenkwamen, hebben plaatsgenomen op grond, en wel zoals eerder de eis was, om maximale afstand van elkaar.
De heren Mark, Hugo en Ernst verheffen zich boven haar op hun gestoelte, kan eigenlijk niet, maar omgekeerd is natuurlijk ook niet netjes, zeker niet in deze tijd.
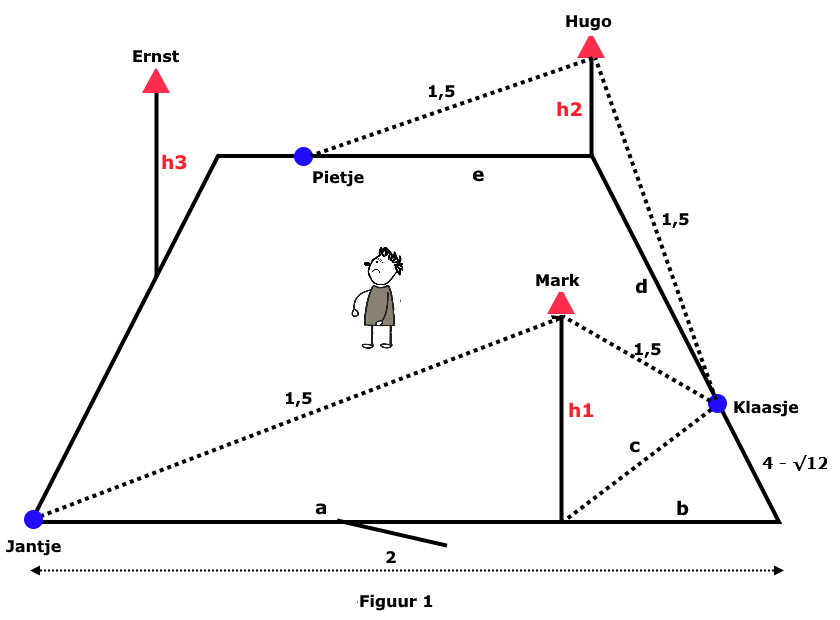
We gaan eerste de stoelhoogte van Mark, als de meest vooraanstaande, berekenen. Hij moet 1,5 meter afstand houden. De afstand Mark-Jantje moet 1,5 (meter) zijn, en ook die van Mark-Klaasje.
We halen weer Pythogoras van stal: de som van de kwadraten van zijden van een rechthoekige driehoek is gelijk aan het kwadraat van de schuine zijde. Dus eenvoudig: enezijde2 + anderezijde2 = schuinezijde2 ; En natuurlijk is zo ook
enezijde2 = schuinezijde2 - anderezijde2
We passen het toe op de hoogte waarop Mark zit t.o.v. Jantje:
h12 + a2 = 1,52 ; of
h12 = 1,52 - a2
Maar Mark wil ook op 1,5 meter afstand van Klaasje houden. Dus weer Pythagoras:
h12 + c2 = 1,52 ; of
h12 = 1,52 - c2
De kunst is uit deze formules a en c weg te werken zodat we uiteindelijk een numerieke waarde voor h1 overhouden. Daarvoor gaan we eerst c buitenboord kieperen, als volgt.
(die 4 - √12 hebben we berekend in Afstand houden – Oplossing 15-01-22.)
c2 = b2 + (4 - √12)2 ; Dus hiermee kunnen we de c2 in de formule vervangen:
h12 = 1,52 - b2 - (4 - √12)2 ;
We weten ook dat b = 2 – a. Zo kan ook de b in de formule worden verwijderd:
h12 = 1,52 - (2-a)2 - (4 - √12)2 ; Even wat friemelen en dan blijkt:
h12 = 1,52 - 4 +4a - a2 - 16 + 8√12 - 12
h12 = 1,52 - 32 +4a - a2 + 8√12
h12 moet dus hieraan voldoen én aan de rode formule boven, er is immers maar 1 hoogte. Daarom
1,52 - a2 = 1,52 - 32 +4a - a2 + 8√12 Even omrommelen:
a = 8 - 2√12
Nu kunnen we eindelijk h1 berekenen:
h12 = 1,52 - (8 - 2√12)2
h1 = √(1,52 - (8 - 2√12)2 )
h1= 1,049405
Dus als Mark gaat zitten op een stoeltje dat net een meter hoog is bewaart hij 1,5 meter afstand tot buurvrouwen Jantje en Klaasje beneden. En dat doet hij graag natuurlijk.
Het geldt trouwens ook voor Ernst want die zit in een precies gelijke situatie. De hoogte van zijn stoeltje h3 is dus ook 1,049405 meter.
Minimale hoogte stoeltje h2
Maar nu Hugo. Hij zit rechtsachter in het hoekje waar vaak de klappen vielen. Deze berekening is eenvoudig(er). Immers we weten:
Afstand stoeltjes van Hugo- Klaasje over de grond gemeten, is d (en die van Hugo-Pietje e). En op z'n stoel moet hij 1,5 meter van Klaasje bewaren. Dus
d = 2 - (4 - √12) = √12 – 2 ; En met Pythagoras is dan
h22 = 1,52 - (√12 - 2)2
h2 = √(1,52 - (√12 - 2)2 )
h2 = 0,3262
Dus voor Hugo is een nederig kinderstoeltje van 32 cm voldoen om afstand van Klaasje en Pietje te houden. Kan hij na het prikken snel weer wat anders gaan doen.
Klaar?
Nu heb ik ook een oplossing binnengekregen van eerder genoemde inzender. Zijn we het rekenkundig eens? Valt er meer nog te overwegen? Bijvoorbeeld het 'geestelijk' element nog een stukje verder uitdiepen misschien?
De volgende keer hopen we de lezers daarmee te verblijden..
